Specifying paths to FCS data¶
To get cracking, we need some flow cytometry data (i.e., .fcs files). A few FCS data files have been bundled with this python package. To use these files, enter the following in your ipython terminal:
In [1]: import FlowCytometryTools
In [2]: from FlowCytometryTools import test_data_dir, test_data_file
In [3]: datadir = test_data_dir
In [4]: datafile = test_data_file
datadir will point to a directory containing flow cytometry data while datafile will point
to a specific FCS file.
To analyze your own data, simply set the ‘datafile’ variable to the path of your .fcs file:
>>> datafile=r'C:\data\my_very_awesome_data.fcs'
Windows Users Windows uses the backslash character (‘’) for paths. However, the backslash character is a special character in python that is used for formatting strings. In order to specify paths correctly, you must precede the path with the character ‘r’.
Good:
>>> datafile=r'C:\data\my_very_awesome_data.fcs'Bad:
>>> datafile='C:\data\my_very_awesome_data.fcs'
Working with individual FCS files¶
Below is a brief description, for more information see FCMeasurement.
Loading the file¶
Once datadir and datafile have been defined, we can proceed to load the data:
In [5]: from FlowCytometryTools import FCMeasurement
In [6]: sample = FCMeasurement(ID='Test Sample', datafile=datafile)
Channel Information¶
Want to know which channels were measured? No problem.
In [7]: print(sample.channel_names)
('HDR-T', 'FSC-A', 'FSC-H', 'FSC-W', 'SSC-A', 'SSC-H', 'SSC-W', 'V2-A', 'V2-H', 'V2-W', 'Y2-A', 'Y2-H', 'Y2-W', 'B1-A', 'B1-H', 'B1-W')
In [8]: print(sample.channels)
$PnB $PnG $PnR $PnN $PnE $PnS
Channel Number
1 32 1 262144 HDR-T [0.000000, 0.000000] HDR-T
2 32 1 262144 FSC-A [0.000000, 0.000000] FSC-A
3 32 1 262144 FSC-H [0.000000, 0.000000] FSC-H
4 32 1 262144 FSC-W [0.000000, 0.000000] FSC-W
5 32 1 262144 SSC-A [0.000000, 0.000000] SSC-A
6 32 1 262144 SSC-H [0.000000, 0.000000] SSC-H
7 32 1 262144 SSC-W [0.000000, 0.000000] SSC-W
8 32 1 262144 V2-A [0.000000, 0.000000] V2-A
9 32 1 262144 V2-H [0.000000, 0.000000] V2-H
10 32 1 262144 V2-W [0.000000, 0.000000] V2-W
11 32 1 262144 Y2-A [0.000000, 0.000000] Y2-A
12 32 1 262144 Y2-H [0.000000, 0.000000] Y2-H
13 32 1 262144 Y2-W [0.000000, 0.000000] Y2-W
14 32 1 262144 B1-A [0.000000, 0.000000] B1-A
15 32 1 262144 B1-H [0.000000, 0.000000] B1-H
16 32 1 262144 B1-W [0.000000, 0.000000] B1-W
Full Meta Data¶
In addition to the raw data, the FCS files contain “meta” information about the measurements, which may be useful for data analysis. You can access this information using the meta property, which will return to you a python dictionary. The meaning of the fields in meta data is explained in the FCS format specifications (google for the specification).
In [9]: print(type(sample.meta))
<class 'dict'>
In [10]: print(sample.meta.keys())
���������������dict_keys(['$OP', '$ENDSTEXT', '$DATE', '$CYTSN', '$FIL', '$ENDDATA', '_channel_names_', '$SRC', '$MODE', '$DATATYPE', '$BEGINANALYSIS', '$CYT', '$PAR', '$TOT', '$ENDANALYSIS', '$BTIM', '$BEGINSTEXT', '__header__', '$CELLS', '$NEXTDATA', '$SYS', '_channels_', '$BYTEORD', '$ETIM', '$BEGINDATA'])
In [11]: print(sample.meta['$SRC'])
�����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������A3
Accessing Raw Data¶
The data is accessible as a pandas.DataFrame.
In [12]: print(type(sample.data))
<class 'pandas.core.frame.DataFrame'>
In [13]: print(sample.data[['Y2-A', 'FSC-A']][:10])
�������������������������������������� Y2-A FSC-A
0 109.946274 459.962982
1 5554.108398 -267.174652
2 81.835281 -201.582336
3 -54.120304 291.259888
4 -10.542595 -397.168579
5 34.791252 -213.151566
6 6132.993164 -25.696339
7 33.034771 61.271519
8 6688.348633 1462.823608
9 14.344463 490.025482
If you do not know how to work with DataFrames, you can get the underlying numpy array using the values property.
In [14]: print(type(sample.data.values))
<class 'numpy.ndarray'>
In [15]: print(sample.data[['Y2-A', 'FSC-A']][:10].values)
������������������������[[ 109.9463 459.963 ]
[5554.1084 -267.1747]
[ 81.8353 -201.5823]
[ -54.1203 291.2599]
[ -10.5426 -397.1686]
[ 34.7913 -213.1516]
[6132.993 -25.6963]
[ 33.0348 61.2715]
[6688.3486 1462.8236]
[ 14.3445 490.0255]]
Of course, working directly with a pandas DataFrame is very convenient. For example,
In [16]: data = sample.data
In [17]: print(data['Y2-A'].describe())
count 10000.000000
mean 2540.119141
std 3330.651123
min -144.069305
25% 10.865871
50% 82.575161
75% 5133.238525
max 68489.953125
Name: Y2-A, dtype: float64
Want to know how many events are in the data?
In [18]: print(data.shape[0])
10000
Want to calculate the median fluorescence level measured on the Y2-A channel?
In [19]: print(data['Y2-A'].median())
82.57516479492188
Transformations¶
The presence of both very dim and very bright cell populations in flow cytometry data can make it difficult to simultaneously visualize both populations on the same plot. To address this problem, flow cytometry analysis programs typically apply a transformation to the data to make it easy to visualize and interpret properly.
Rather than having this transformation applied automatically and without your knowledge, this package provides a few of the common transformations (e.g., hlog, tlog), but ultimately leaves it up to you to decide how to manipulate your data.
As an example, let’s apply the ‘hlog’ transformation to the Y2-A, B1-A and
V2-A channels, and save the transformed sample in tsample.
In [20]: tsample = sample.transform('hlog', channels=['Y2-A', 'B1-A', 'V2-A'], b=500.0)
In the hlog transformation, the parameter b controls the location where the transformation shifts from linear to log. The optimal value for this parameter depends on the range of your data. For smaller ranges, try smaller values of b. So if your population doesn’t show up well, just adjust b.
For more information see FCMeasurement.transform(), FlowCytometryTools.core.transforms.hlog().
Throughout the rest of the tutorial we’ll always be working with hlog-transformed data.
Note
For more details see the API documentation section.
- You can read more about transformations here:
- Bagwell. Cytometry Part A, 2005.
- Parks, Roederer, and Moore. Cytometry Part A, 2006.
- Trotter, Joseph. In Current Protocols in Cytometry. John Wiley & Sons, Inc., 2001.
Plotting¶
Let’s import matplotlib’s plotting functions.
In [21]: from pylab import *
For more information see FCMeasurement.plot().
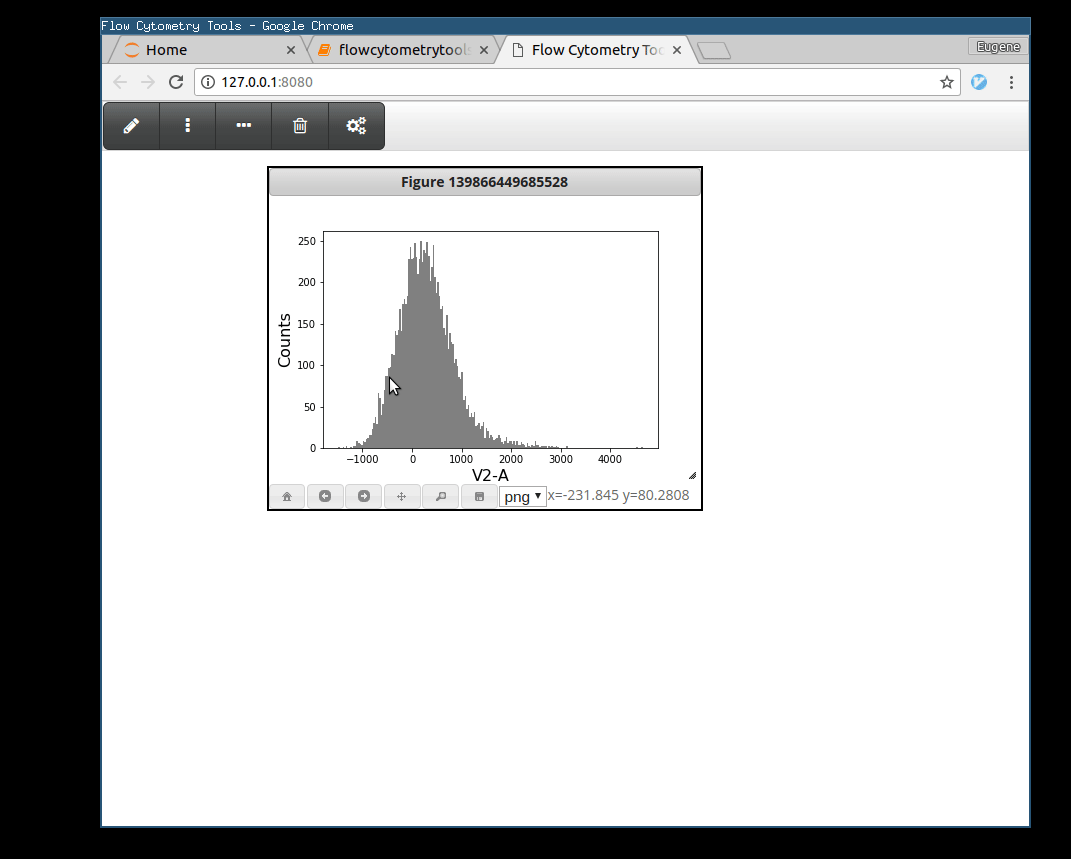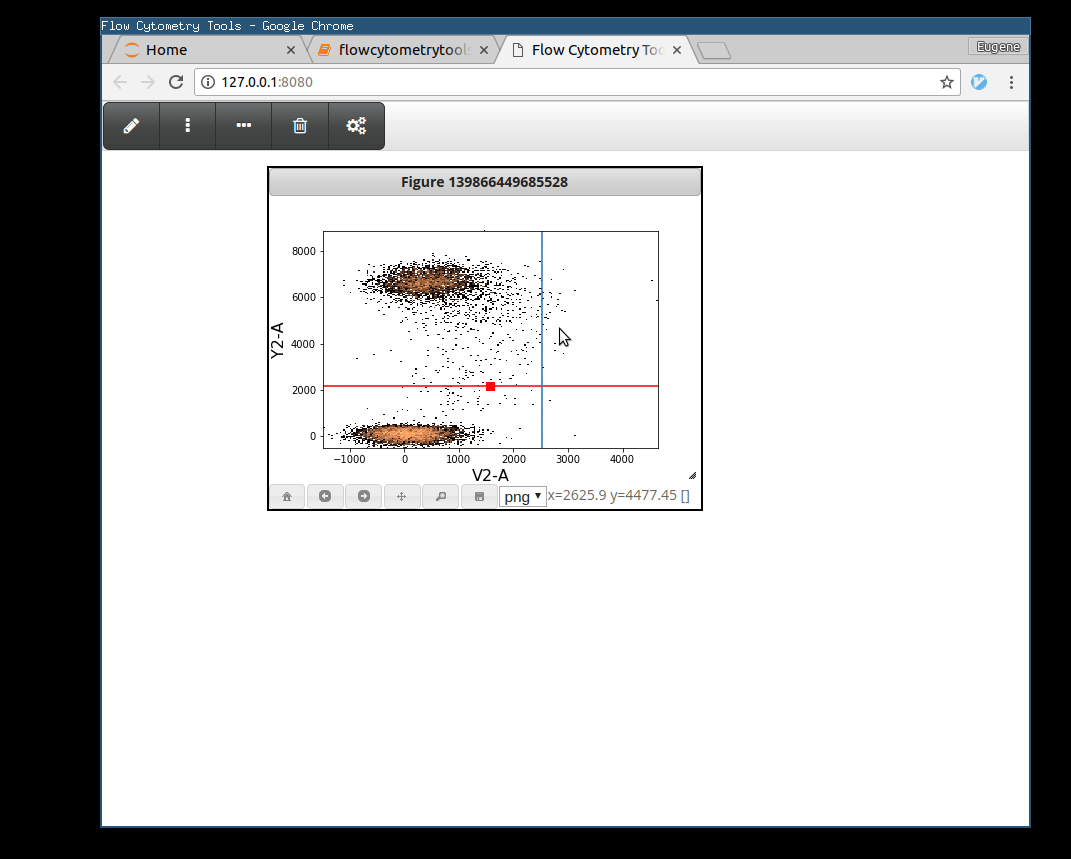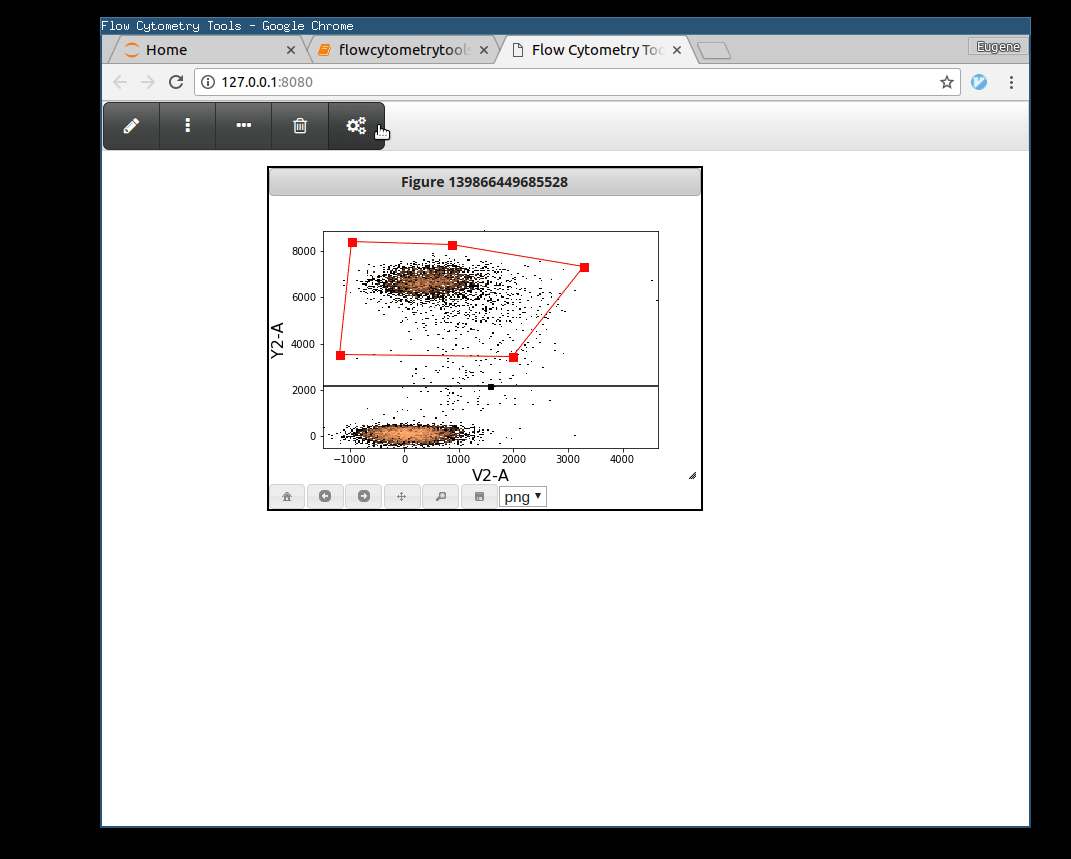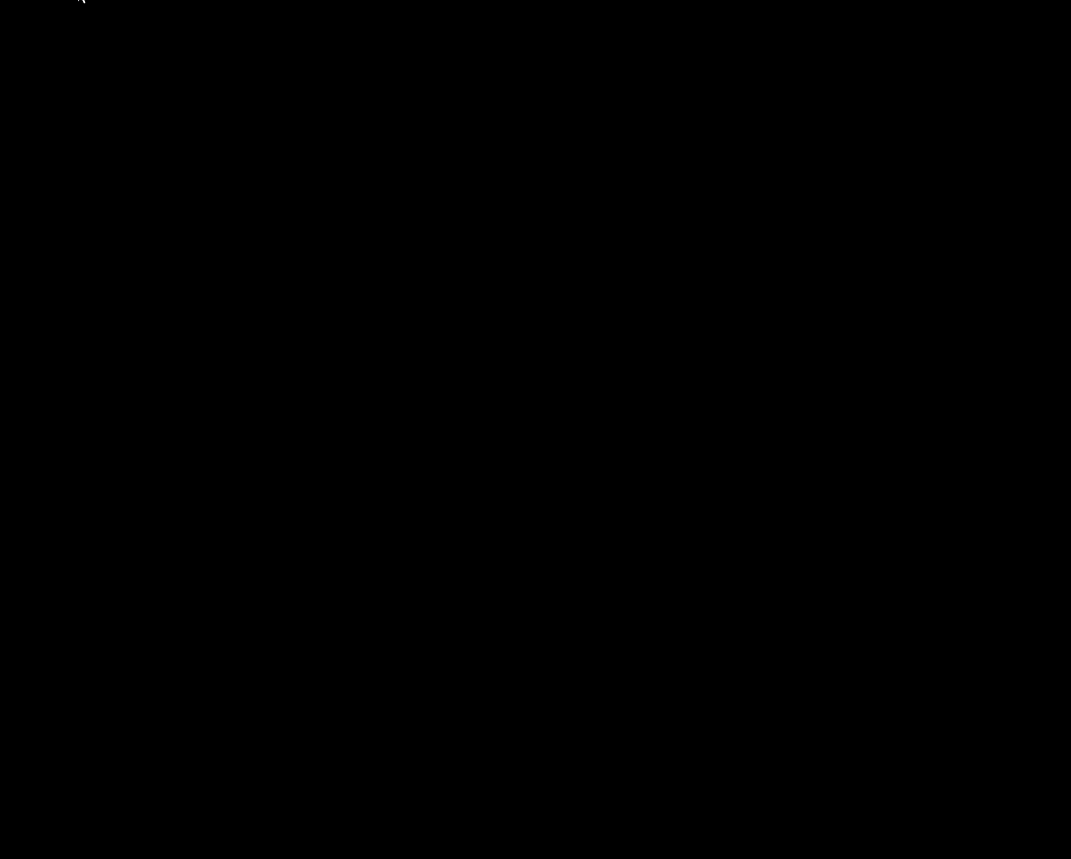
1d histograms¶
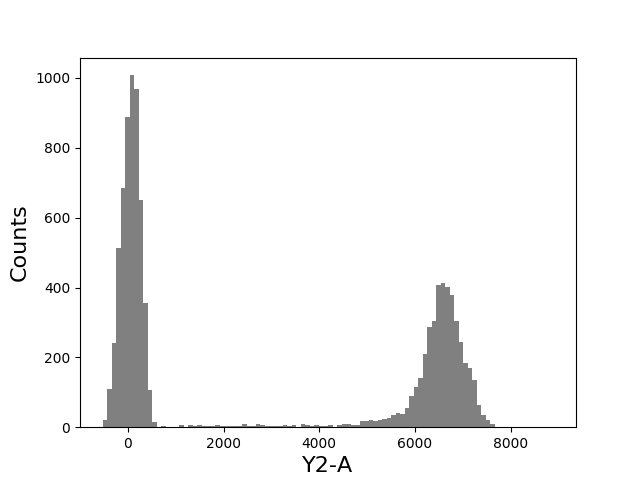
In [22]: figure();
In [23]: tsample.plot(['Y2-A'], bins=100);
In [24]: figure();
In [25]: grid(True);
In [26]: tsample.plot(['Y2-A'], color='green', alpha=0.7, bins=100);

2d histograms¶
If you provide the plot function with the names of two channels, you’ll get a 2d histogram.
In [27]: figure();
In [28]: tsample.plot(['B1-A', 'Y2-A']);
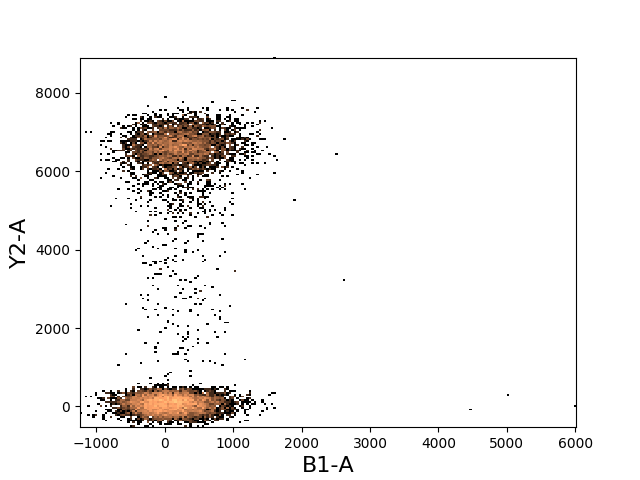
As with 1d histograms, the plot function accepts all the same arguments as does the matplotlib histogram function.
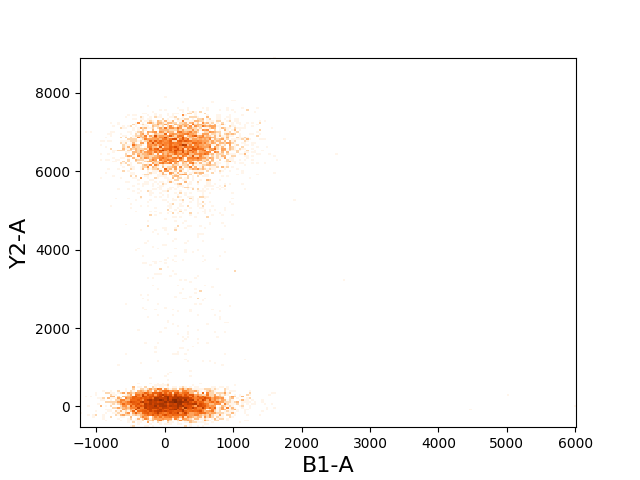
In [29]: figure();
In [30]: tsample.plot(['B1-A', 'Y2-A'], cmap=cm.Oranges, colorbar=False);
2d scatter plots¶
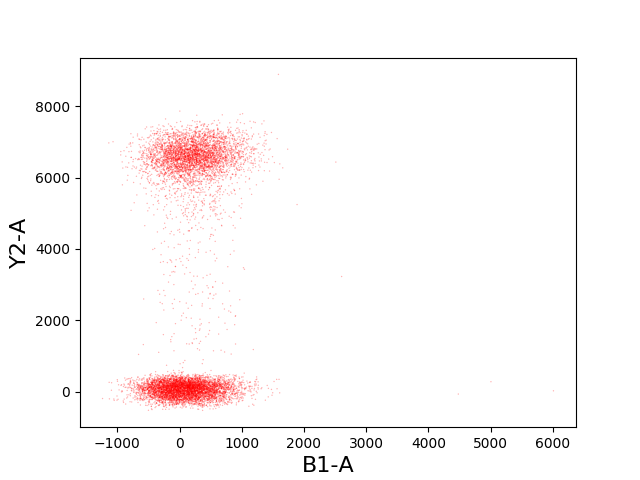
To create a scatter plot, provide the argument kind='scatter to the plot command.
This makes the plot function behave like the matplotlib scatter function (and accept all the same arguments).
In [31]: figure();
In [32]: tsample.plot(['B1-A', 'Y2-A'], kind='scatter', color='red', s=1, alpha=0.3);
Gating¶
See the API for a list of available gates.
Let’s import a few of those gates.
In [33]: from FlowCytometryTools import ThresholdGate, PolyGate
Creating Gates¶
Programmatically¶
To create a gate you need to provide the following information:
- set(s) of coordinates
- name(s) of channel(s)
- region
Let’s create a ThresholdGate that passes events with a Y2-A (RFP) value above the 1000.0.
In [34]: y2_gate = ThresholdGate(1000.0, ['Y2-A'], region='above')
While we’re at it, here’s another gate for events with a B1-A value (CFP) above 2000.0.
In [35]: b1_gate = ThresholdGate(2000.0, ['B1-A'], region='above')
Using the GUI¶
You can launch the GUI for creating the gates, by calling the view_interactively() method of an FCMeasurement instance.
There are two backends enabled for the GUI. Both are buggy, but can help to get the job done.
Use the wx backend this way:
>>> tsample.view_interactively(backend='wx')
Warning
wxpython must be installed in order to use the GUI. (It may already be installed, so just try it out.)
Please note that there’s no way to apply transformations through the GUI, so view samples through the view_interactively method. (Don’t load new FCS files directly from the GUI, if you need those files transformed.)
Use the webagg backend this way:
>>> tsample.view_interactively(backend='webagg')
Plotting Gates¶
In [36]: figure();
In [37]: tsample.plot(['Y2-A'], gates=[y2_gate], bins=100);
In [38]: title('Gate Plotted');
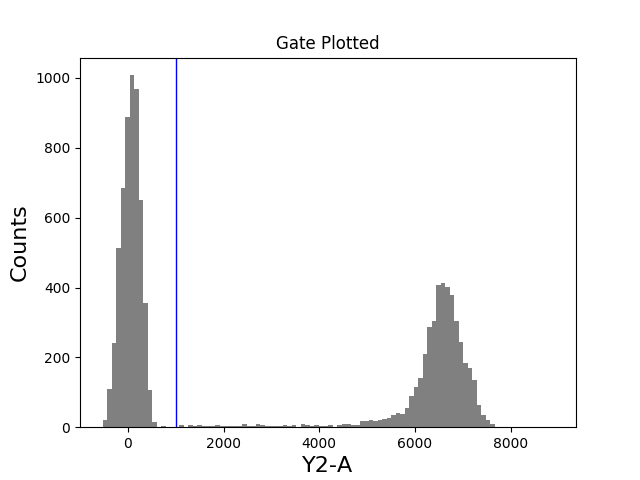
Applying Gates¶
In [39]: gated_sample = tsample.gate(y2_gate)
In [40]: print(gated_sample.get_data().shape[0])
4433
The gated_sample is also an instance of FCMeasurement, so it supports the
same routines as does the ungated sample. For example, we can plot it:
In [41]: figure();
In [42]: gated_sample.plot(['Y2-A'], color='y', bins=100);
In [43]: title('Gated Sample');

Let’s compare the gated and ungated side by side.
In [44]: figure();
In [45]: subplots_adjust(hspace=0.4)
In [46]: ax1 = subplot(211)
In [47]: tsample.plot(['Y2-A'], color='gray', bins=100, gates=[y2_gate]);
In [48]: title('Original Sample');
In [49]: ax2 = subplot(212, sharey=ax1, sharex=ax1)
In [50]: gated_sample.plot(['Y2-A'], color='y', bins=100, gates=[y2_gate]);
In [51]: title('Gated Sample');
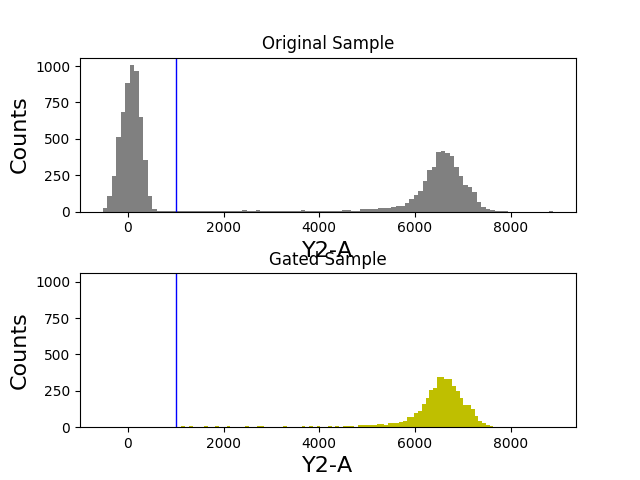
Combining gates¶
Gates can be inverted and combined together. See FlowCytometryTools.core.gates.CompositeGate.
Working with plates¶
For high-throughput analysis of flow cytometery data, loading single FCS files is silly. Don’t be silly!
Instead, we provided you with the awesome FCPlate class (also called FCOrderedCollection).
Loading Data¶
The code below loads two FCS samples and shows two different methods of placing them on a plate container.
In [52]: from FlowCytometryTools import FCPlate
In [53]: sample1 = FCMeasurement('B1', datafile=datafile)
In [54]: sample2 = FCMeasurement('D2', datafile=datafile)
# Use the samples ID as their position on a plate:
In [55]: plate1 = FCPlate('demo plate', [sample1, sample2], 'name', shape=(4, 3))
In [56]: print(plate1)
ID:
demo plate
Data:
1 2 3
A
B B1
C
D D2
Alternatively, one can specify the sample positions independent of the samples IDs using a dictionary:
In [57]: plate2 = FCPlate('demo plate', {'C2' : sample1, 'C3' : sample2}, 'name', shape=(4, 3))
In [58]: print(plate2)
ID:
demo plate
Data:
1 2 3
A
B
C B1 D2
D
In [59]: print(plate2['C2'])
����������������������������������������������������������������������������������<FCMeasurement 'B1'>
Having overwritten the default mapping based on the samples ID, we now have to access sample1 using the key C2. So the command plate['C2'] should return sample1 (whose ID should still remain B1).
In [60]: plate3 = FCPlate('demo plate', {3 : sample1, 4 : sample2}, 'row_first_enumerator', shape=(4, 3))
In [61]: print(plate3)
ID:
demo plate
Data:
1 2 3
A
B
C B1
D D2
In [62]: print(plate3[3])
������������������������������������������������������������������������<FCMeasurement 'B1'>
Note
Below we show a much faster way of loading data into a plate format. This method should make life simpler for most users by removing a bunch of boilerplate code. So keep on reading!
Loading Data (better way)¶
What we’d like to do is to construct a flow cytometry plate object by loading all the ‘*.fcs’ files in a directory.
To do that, FCPlate needs to know where on the plate each file belongs; i.e., we need to tell it that the file ‘My_awesome_data_Well_C9.fcs’ corresponds to well ‘C9’, which corresponds to the third row and the ninth column on the plate.
The process by which the filename is mapped to a position on the plate is the following:
- The filename is fed into a parser which extracts a key from it. For example, given ‘My_awesome_data_Well_C9.fcs’, the parser returns ‘C9’
- The key is fed into a position mapper which returns a matrix position. For example, given ‘C9’ the position_mapper should return (2, 8). The reason it’s (2, 8) rather than (3, 9) is because counting starts from 0 rather than 1. (So ‘A’ corresponds to 0.)
Here’s a summary table that’ll help you decide what to do (depending on your file name format):
| File Name Format | parser | Comments |
|---|---|---|
| ‘[whatever]_Well_C9_[blah].fcs’ | ‘name’ | |
| ‘[blah]_someothertagC9_[blah].fcs’ | ‘name’ | But to use must modify ID_kwargs (see API) for details |
| ‘[whatever].025.fcs’ | ‘number’ | 001 -> A1, 002 -> B1, … etc. i.e., advances by row first |
| Some other naming format | dict | dict with keys = filenames, values = positions |
| Some other naming format | function | Provide a function that accepts a filename and returns a position (e.g., ‘C9’) |
For the analysis below, we’ll be using the ‘name’ parser since our files match that convention. OK. Let’s try it out:
In [63]: from FlowCytometryTools import FCPlate
In [64]: plate = FCPlate.from_dir(ID='Demo Plate', path=datadir, parser='name')
In [65]: plate = plate.transform('hlog', channels=['Y2-A', 'B1-A'])
Let’s see what data got loaded.
In [66]: print(plate)
ID:
Demo Plate
Data:
1 2 3 4 5 6 7 8 9 10 11 12
A A3 A4 A6 A7
B B3 B4
C C7
D
E
F
G
H
And just to confirm, let’s look at the naming of our files to see that parser='name' should indeed work.
In [67]: import os
In [68]: print(os.path.basename(plate['A3'].datafile))
RFP_Well_A3.fcs
This plate contains many empty rows and columns. The method FCPlate.dropna() allow us to drop empty rows and columns for convenience:
In [69]: plate = plate.dropna()
In [70]: print(plate)
ID:
Demo Plate
Data:
3 4 6 7
A A3 A4 A6 A7
B B3 B4
C C7
Plotting¶
Please import matplotlib’s plotting functions if you haven’t yet…
In [71]: from pylab import *
For more information see FCPlate.plot().
In [72]: figure();
In [73]: plate.plot(['Y2-A'], bins=100);

In [74]: figure();
In [75]: plate.plot(['B1-A', 'Y2-A'], bins=100, wspace=0.2, hspace=0.2);
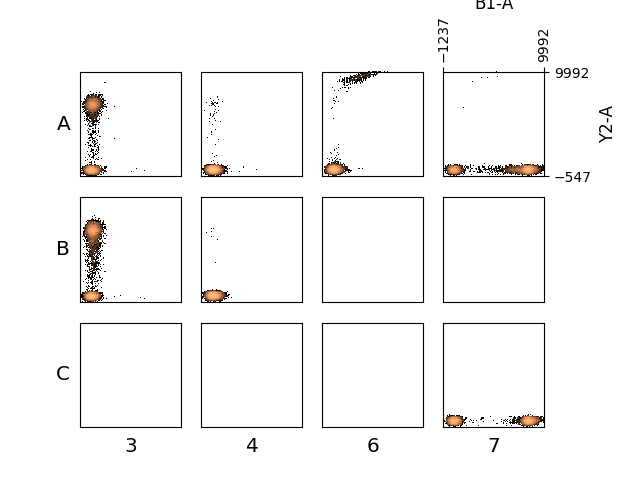
Accessing Single Wells¶
FCPlate supports indexing to make it easier to work with single wells.
In [76]: print(plate['A3'])
<FCMeasurement 'A3'>
In [77]: figure();
In [78]: plate['A3'].plot(['Y2-A'], bins=100);
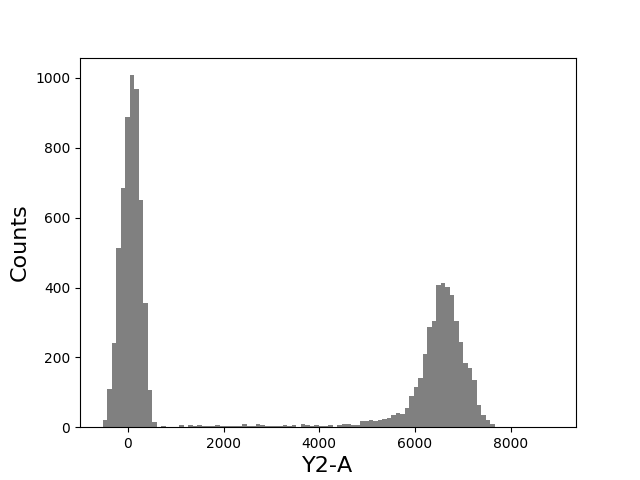
Examples¶
Counting using the counts method¶
Use the counts method to count total number of events.
In [79]: total_counts = plate.counts()
In [80]: print(total_counts)
3 4 6 7
A 10000.0 10000.0 10000.0 10000.0
B 10000.0 10000.0 NaN NaN
C NaN NaN NaN 10000.0
Let’s count the number of events that pass a certain gate:
In [81]: y2_counts = plate.gate(y2_gate).counts()
In [82]: print(y2_counts)
3 4 6 7
A 4433.0 50.0 420.0 6.0
B 5496.0 7.0 NaN NaN
C NaN NaN NaN 0.0
What about the events that land outside the y2_gate?
In [83]: outside_of_y2_counts = plate.gate(~y2_gate).counts()
In [84]: print(outside_of_y2_counts)
3 4 6 7
A 5567.0 9950.0 9580.0 9994.0
B 4504.0 9993.0 NaN NaN
C NaN NaN NaN 10000.0
Counting on our own¶
To learn how to do more complex calculations, let’s start by writing our
own counting function. At the end of this, we better get the
same result as was produced using the counts method above.
Here’s the function:
In [85]: def count_events(well):
....: """ Counts the number of events inside of a well. """
....: data = well.get_data()
....: count = data.shape[0]
....: return count
....:
Let’s check that it works on a single well.
In [86]: print(count_events(plate['A3']))
10000
Now, to use it in a calculation we need to feed it to the apply method.
Like this:
In [87]: print(plate['A3'].apply(count_events))
10000
The apply method is a functional, which is just a fancy way of saying
that it accepts functions as inputs. If you’ve got a function that can
operate on a well (like the function count_events), you can feed it into the apply
method. Check the API for the apply method for more details.
Anyway, the apply method is particularly useful because it works on plates.
In [88]: total_counts_using_our_function = plate.apply(count_events)
In [89]: print(type(total_counts_using_our_function))
<class 'pandas.core.frame.DataFrame'>
In [90]: print(total_counts_using_our_function)
�������������������������������������� 3 4 6 7
A 10000.0 10000.0 10000.0 10000.0
B 10000.0 10000.0 NaN NaN
C NaN NaN NaN 10000.0
Holy Rabbit!
First, for wells without data, a nan was produced.
Second, the output that was returned is a DataFrame.
Also, as you can see the total counts we computed (total_counts_using_our_function)
agrees with the counts computed using the counts methods in the previous example.
Now, let’s apply a gate and count again.
In [91]: print(plate.gate(y2_gate).apply(count_events))
3 4 6 7
A 4433.0 50.0 420.0 6.0
B 5496.0 7.0 NaN NaN
C NaN NaN NaN 0.0
Calculating median fluorescence¶
Ready for some more baking?
Let’s calculate the median Y2-A fluorescence.
In [92]: def calculate_median_rfp(well):
....: """ Calculates the median on the RFP channel. """
....: data = well.get_data()
....: return data['Y2-A'].median()
....:
The median rfp fluorescence for all events in well ‘A3’.
In [93]: print(calculate_median_rfp(plate['A3']))
303.09112548828125
The median rfp fluorescence for all events in the plate is:
In [94]: print(plate.apply(calculate_median_rfp))
3 4 6 7
A 303.091125 105.875381 136.326202 104.436157
B 4701.629395 126.765717 NaN NaN
C NaN NaN NaN 97.277603
The median rfp fluorescence for all events that pass the y2_gate is:
In [95]: print(plate.gate(y2_gate).apply(calculate_median_rfp))
3 4 6 7
A 6573.452148 6240.961426 9346.646484 9294.400391
B 6544.949219 6413.048340 NaN NaN
C NaN NaN NaN NaN
